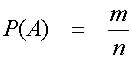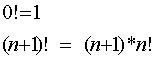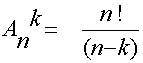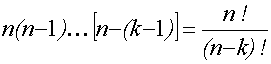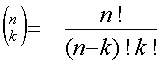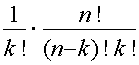1.1 Joukko-oppilisia käsitteitä
Joukolatarkoitetaan
tiettyjen asioiden, esineiden lukujen jne. yhdelmää. Mainittuja
joukon jäseniä sanotaan sen alkioksi tai elementeiksi.
Alkioiden määrä voi olla äärellinen tai äretön.
Joukkoa, jossa ei ole yhtään alkiota, sanotaan tyhjäksi
joukoksi?.
Joukon ilmaiseminen
voi tapahtua eri tavoilla luettelemassa kaikki alkiot. Esimerkiksi nopan
silmälukujen joukko A voidaan esittää muodossa
A = { 1,2,3,4,5,6 }
Myös
voidaan käyttää merkintääA
= { x| x kokonaisluku, 1 < x
<
6
}
Jos
alkio a kuuluu joukkoon A käytetään merkintääa A A
Merkintä
B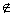 A Ilmaisee,
että B ei kuulu joukkoon A A Ilmaisee,
että B ei kuulu joukkoon A
Osa- ja perusjouko
Jos jokainen joukon
B alkio on myös joukon A alkio, joukko B on joukon A osajoukko, mikä
ilmaistaan merkinnällä
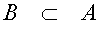
1.2 Tödennäköisyyden idea
SatunnaisilmiönS tapahtuman
A
todennäköisyydellä tarkoitetaan lukua P(A), joka ilmaisee
odotettavissa olevien A:n sattumiskertojen suhteellisen osuuden S:n tapahtuessa
hyvin monta kertaa.
Klassisen
todennäköiseyyden määrittely edellyttää,
että tulosmahdollisuuksien määrä on äärellinen
ja että tulosmahdollisuudet ovat symmetrisiä. Jos tapausta A
vastaavien symmetristen alkeistapauksien lukumäärä on m,
on todennäköisyys
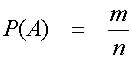
missän on
sattunnaisilmiönS kaikkien
alkeistapauksien lukumäärä.
Todennäköisyyslaskennan peruskäsitteitä
Tapahtumaa
tai ilmiötä, jonka tuloksen määrää sattuma,
kutsutaan satunnaisilmiöksi. Jos se tehdään,
esimerkiksi heitetään noppaa, kutsutaan tekoa satunnaiskokeeksi.
Satunnaisilmiön
mahdollisia tuloksia kutsutaan alkeistapauksiksi ja koko alkeistapausten
joukkoa perusjoukoksi. Perusjoukon osajoukkoa kutsutaan tapahtumaksi.
Tapahtumaan kuuluvia alkeistapauksia kutsutaan suotuisiksi alkeistapahtumiksi.
Jos kaikki
perusjoukon alkeistapaukset ovat yhtä todennäköisyyksiä,
kuten lottoarvonnassa arvotut luvut, kutsutaan alkeistapauksia symmetrisiksi.
Tapahtuma,
jolla ei ole yhtään suotuista alkeistapahtumaa, esimerkiksi nopan
heitossa saada silmäluku 7, kutsutaan mahdottomaksi tapahtumaksi.
Jos kaikki perusjoukon alkeistapaukset ovat suotuisia, tapahtumaa kutsutaan
varmaksi
tapahtumaksi.
TODENNÄKÖISYYS
on tiheysfunktion kuvaajan ja x-akselin väliin jäävän
alueen pinta-ala, eli määrätty integraali.
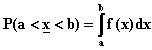 
Harjoitustehtavia
Virheettömät arpakuutiot
| 1.2.1. Yhden silmäluvun todennäköisyys
Kun arpakuutiota heitetään kerran, mikä on todennäköisyys,
että heiton tuloksena saadaan viisi? |
Ratkaisu.
Alkeistapauksia on kuusi ("heiton tulos 1" ,"heiton tulos
2",..)
Koska arpakuutio oli virheetön, niin jokaisen alkeistapauksen
todennäköisyys on 1/6 eli P({5}) = 1/6. |
| 1.2. 2. Kahden arpakuution heitto. Kun heitetään
kahta arpakuutiota, niin mikä on todennäköisyys, että
saadaan pari ? |
Ratkaisu .
Kahden arpanopan heitossa mahdolliset alkeistapaukset
laitetaan taulukoon siten , että rivillä on toisen arpanopan
alkeistapaukset ja sarakkeissa vastaavasti toisen nopan alkeistapaukset.

Alkeistapauksia on nyt 6*6=36. Suotuisia tapauksia eli
sellaisia tapauksia, missä arpanoppien silmäluvut ovat samat
on (1,1), (2,2), (3,3), (4,4), (5,5) ja (6,6) kuusi kappaletta. Todennäköisyys,
että saadaan kahdella nopalla pari on siis P({pari})= 6/36 = 1/6 |
Pelikorttipakka. Nostetun kortin todennäköisyys
1.2.3. Pelikorttipakassa on 52 korttia, jotka on
jaettu neljään maahan: hertta, pata, risti ja ruutu. Jokaisessa
maassa on kolmetoista korttia, jotka ovat numerokortit
A=1, 2,3,4,5,6,7,8,9 ja 10 sekä kolme kuvakorttia
J=11, Q=12 ja K=13.
Pakasta nostetaan kortti, mikä on todennäköisyys,
että nostettu kortti on
a) kuningas eli K
b) hertta kuningatar " Q
c) pistearvoltaan suurempi kuin 10
d) pistearvoltaan pienempi tai yhtäsuuri kuin 10 |
Ratkaisu
Alkeistapauksia korttipakassa on 52 kappaletta.
a) kuninkaita pakassa on neljä, joten P({K}) = 4/52
= 0,077
b) herttakuningatarta on yksi, joten P({ª Q }) =
1/52 = 0,019
c) pistearvoltaan suurempia kuin 10 ovat kuvakortit neljästä
maasta 4*3 = 12, joten, P({>10}) = 12/52 = 0,23
d) pistearvoltaan pienempiä tai yhtäsuuria kuin
10 on edellisen tapahtuman komplementti- eli vastatapahtuma eli P({ *10})
= 1-P({>10}) = (52-12) / 52 = 40 / 52 = 1 - 0,23 = 0,77 |
|
| Tilastollinen todennäköisyys |
| 1.2.4. Syntyvän
lapsen sukupuoli. Kuinka voidaan laskea syntyvän lapsen sukupuolen
todennäköisyys, kun tapahtuma ei ole symmetrinen? |
| Ratkaisu . Syntyvän lapsen sukupuoli voitaisiin
määrittää klassisen todennäköisyystulkinnan
avulla. Silloin otosavaruus koostuisi kahdesta alkeistapauksesta {tyttö}
ja {poika}, joiden todennäköisyydet ovat yhtäsuuret P({tyttö})
= P({poika}) = 1/2. Mutta todellisuudessa syntyvän lapsen sukupuoli
ei ole symmetrinen tapahtuma, vaan poikia syntyy enemmän kuin tyttöjä
- suomalaisten syntyvien lasten sukupuolijakauma on: tyttöjä
noin 49% ja poikia 51%. Tällaisessa tapauksessa todennäköisyyden
määrittäminen tehdään todennäköisyyden
frekvenssitulkinnan avulla. Tätä tapaa kutsutaan myös tilastolliseksi
todennäköisyydeksi. Suomen syntyvyystilaston mukaan syntyneiden
lasten sukupuolijakaumat vuosina 1990-97 olivat (Suomen tilastollinen vuosikirja
,1998)

Yksittäisen vuoden kohdalla tyttöjen osuus vaihtelee
48,71%:sta 49,19%:een. Kun vuodet yhdistetään niin saadaan tyttöjen
osuudeksi 48,98%, mikä vastaa suurten kansainvälisten tutkimusten
mukaisesti syntyneiden tyttöjen osuutta eli Suomessa vuosina 1990-97
poikien syntyvyysenemyydeksi saadaan (510 851 - 250 227) : 250 227 = 260
624 / 250 227 * 1,042 eli 1 042 poikaa syntyy jokaista 1 000 tyttöä
kohti.
|
.
|
|
|
|
Lukun-keroma
on n :
n ensimmäisen positiivisen kokonaisluvun tulo
n!
= 1*2*3*... n,
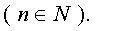
N
-positiivisten
kokonaiskukujen joukko. Lisäksi sopimuksen mukaan
0!
= 1.
N-kertomavoidaan
induktiivisesti määritellä yhtälöparilla
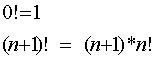
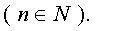
Permutaatiot
JoukonE
= {a1,
a2, . . . an}
permutaatiolla
tarkoitetaan jokaista sen alkioista muodostettava järjestettyä
jonoa, esimerkiksi ( an, an-1, . . . a2,a1
).
Lause:
Jos joukossa on n alkiota, niiden permutaatiota on n!.
Esimerkki:
3-alkiosella joukolla E
= {a, b, c }
on 3! =
6 permutaatiota:
( a,
b, c)( a, c, b )
( b,
c, a )( b, a, c )
( c,
a, b )( c, d, a )
Variaatiot
JoukonE
= {a1,
a2, . . . an}
k : ttain muodostettuilla variaatioilla tarkoitetaanE
:
n järjestettyjä osajoukkoja, joissa on k alkiota.
Lause:
JoukonE n alkion k : ttain otettujen
variaatioiden määrä on
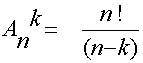
Todistus seuraa tuloperiaatteesta:1.
jäsen voidaan valitan tavalla,
2. jäsen n-1 tavalla jne. Tuloksesi saadaan
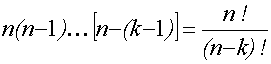
Kombinaatiot
JoukonE
= {a1,
a2, . . . an}
k : ttain muodostettuilla kombnaatioilla tarkoitetaanE
:
n josajoukkoja, joissa on k alkiota.
Lause:
JoukonE n alkion k : ttain
otettujen kombinaatioiden lukumäärä on
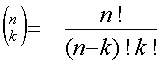
Todistus
: k : ttain otettua kombinaatiota vastaa k !variaatiota,
joten kysytty kombinatioitten määrä on vain
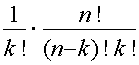 eli
binomikerroin eli
binomikerroin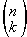 . .
|
Yhdiste (unioni) 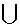
Tapahtumien
A ja B yhdiste (unioni)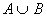 on
tapahtuma, missä A tai Btai
molemmat sattuu. on
tapahtuma, missä A tai Btai
molemmat sattuu.
Lekkaus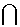 A
ja B A
ja B
Tapahtumien
A ja B leikkau s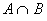 on
tapahtuma, missä A ja B sattuu. on
tapahtuma, missä A ja B sattuu.
Komplementti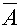
Tapahtuman
A komplementti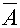 0n
tapahtuma, missä A ei satu. 0n
tapahtuma, missä A ei satu.
Erotus
A\ B
Tapahtumien
A ja B erotus A\B on tapahtuma, missä A sattuu, mutta B ei satu
Kertolasku- ja yhteenlaskusäännöt
Tapahtumia kutsutaan riippumattomiksi, jos jonkun tapahtuman
todennäköisyys ei riipu toisen tapahtuman tapahtumisesta tai
ei-tapahtumisesta eli toisen tapahtuman tapahtuminen ei vaikuta toisen
tapahtuman todennäköisyyteen. Esimerkiksi kahta noppaa heitettäessä
toisen silmäluku ei vaikuta siihen mikä silmäluku toiseen
noppaan tulee.
Riippumattomien tapahtumien kertolaskusääntö
Jos tapahtumat ovat toisistaan riippumattomia tapahtumia,
silloin todennäköisyys, että kaikki nämä tapahtumat
tapahtuu on kunkin tapahtuman todennäköisyyksien tulo.

Yhteenlaskusääntö
Todennäköisyyslaskennan yhteenlaskusääntö
on kahden tapahtuman A ja B tapauksessa
P(A tai B) = P(A) + P(B) - P(A ja B).
Kun tapahtumat ovat erillisiä eli tapahtumat A ja
B ovat toisensa poissulkevia eli A:lla ja B:lla ei ole yhteisiä alkeistapauksia,
niin poissulkevien tapahtumien yhteenlaskusäännöksi saadaan
P(A tai B) = P(A) + P(B).
Yleisessä muodossa yhteenlaskusääntö
erillisille tapahtumille on
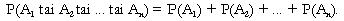
Harjoitustehtäviä
| Tuloperiaate |
1.3.1 Lasten syntymäkuukaudet
Niemisen perheessä on kolme lasta, joista ketkään
eivät ole keskenään kaksosia. Mikä on todennäköisyys,
että
a) kaikki kolme lasta ovat syntyneet eri kuukausina
b) ainakin kaksi on syntynyt samassa kuussa ?
|
Ratkaisu 1.3.1.
Syntymiskuukaudet muodostavat kolmen kuukauden jonon
esimerkiksi tammikuu, kesäkuu, tammikuu.
Alkeistapauksiksi valitaan kaikki kolmen kuukauden jonot,
joiden lukumäärät voidaan laskea tuloperiaatteella
1. kuukausi 12 vaihtoehtoa, 2. kuukausi 12 vaihtoehtoa
ja 3. kuukausi 12 vaihtoehtoa. Joten jonojen lukumääräksi
saadaan 
a) Kun lasketaan tapahtumalle "kaikki lapset ovat syntyneet
eri kuukausina" todennäköisyyttä, lasketaan suotuisten tapahtumien
eli suotuisten jonojen lukumäärä samoin tuloperiaatteella
1. kuukausi 12 vaihtoehtoa,
2. kuukausi 11 vaihtoehtoa eli eri kuukautta kuin edellinen
ja
3. kuukausi 10 vaihtoehtoa eli eri kuukautta kuin edelliset.
Suotuisia jonoja on siis kaikkiaan 12 * 11 * 10 = 1 320
jonoa. Todennäköisyys, että kaikki lapset ovat syntyneet
eri kuukausina on siis P({kaikki lapset syntyneet eri kuukausina}) = 1
320 / 1 728 * 0,76
b) Tapahtumalle "ainakin kaksi lasta on syntynyt samassa
kuussa" suotuisia tapauksia ovat ne kolmen kuukauden jonot, joissa jokin
kuukausi toistuu, kuten tehtävän ratkaisun alussa olevassa esimerkissä,
missä lapset olivat syntyneet tammikuussa, kesäkuussa ja tammikuussa.
Näiden suotuisien tapahtumien lukumäärä
on kaikkien jonojen lukumäärästä vähennetään
ne jonot, joissa kaikki lapset olivat syntyneet eri kuukausina.
Toisin sanoen tämä tapahtuma on a-kohdan tapahtuman
vastatapahtuma, joka saadaan P({Ainakin kaksi lasta on syntynyt samassa
kuussa}) = 1 - P({Kaikki lapset ovat syntyneet eri kuussa})
Toisaalta ratkaisu voidaan laskea myös suotuisten
tapahtumien lukumäärällä, joita tässä tapauksessa
on 123 - (12 * 11 * 10) = 1 728 - 1 320 = 408,
joten todennäköisyys, että ainakin kaksi
lasta on syntynyt samassa kuussa on P({Ainakin kaksi lasta}) = 408 / 1
728 = 1 - (1 320 / 1 728) * 1 - 0,76 = 0,24 |
1.3.2. Vedonlyönti
Löisitkö vetoa sen puolesta, että
a) kolmea noppaa heitettäessä kaikissa nopissa
olisi eri silmäluvut
b) kolmen vedetyn kortin joukossa olisi ainakin yksi
kuvakortti (K, Q tai J)? |
Ratkaisu 1.3.2.
a) Kolmen nopan heitto
Kolmen nopan heiton silmäluvut muodostavat jonon
esimerkiksi 1, 5, 3. Näitä kaikkia kolmen silmäluvun jonoja
voidaan pitää alkeistapauksina. Kaikkiaan kolmen silmäluvun
jonoja tulee
1. silmäluku 6 vaihtoehtoa,
2. silmäluku 6 vaihtoehtoa ja
3. silmäluku 6.vaihtoehtoa eli
kaikkiaan kolmen silmäluvun jonojen lukumääräksi
tulee
6* 6* 6 = 216.
Suotuisia alkeistapauksia ovat kolmen silmäluvun
jonoista ne, joissa silmäluvut ovat erisuuria. Tällaisia jonoja
on
1.silmäluku 6 vaihtoehtoa,
2.silmäluku 5 vaihtoehtoa (eri silmäluku kuin
edellinen) ja
3.silmäluku 4 vaihtoehtoa (eri silmälukua kuin
edelliset) eli
6* 5* 4 = 120.
Todennäköisyys, että kaikissa kolmessa
nopassa on eri silmäluku on siis
P({kolmen nopan silmäluvut erisuuria}) = 120 : 216 * 0,56 > 0,50
eli koska todennäköisyys on suurempi kuin 0,50
kannattaa lyödä kolmen eri suuren silmäluvun puolesta vetoa.
b) Kolmen korttia muodostavat jonoa voidaan pitää
alkeistapauksena.
Vastaavasti kuten a)-kohdassa näitä alkeistapauksia
on kaikkiaan
13* 13* 13 = 2 197.
Suotuisia tapauksia tapahtumalle, että kaikki kolme
korttia ovat muita kuin kuvakortteja on
10* 10* 10 = 1 000.
Todennäköisyys, että kaikki kolme korttia
eivät ole kuvakortteja
P({kolme ei-kuvakorttia}) = 1 000 : 2 197 * 0,46
ja vastatapahtuman todennäköisyys on
P({ainakin yksi kuvakortti)} = 1 - P({kolme ei-kuvakorttia}) = 1 - 0,46
= 0,54 > 0,50
joten kannattaa lyödä vetoa, että tulee
vähintään yksi kuvakortti.
Jos joukossa on n alkiota, sen alkiot voidaan järjestää
jonoon n! eri tavalla. n! tarkoittaa sitä, että kun valitaan
ensimmäinen alkio, meillä on valittavana n
eri alkiota,
toisen valintaan meillä n-1 eri alkioita
ja niin edelleen aina viimeisen alkion valintaan saakka,
jolloin meillä on enää 1 alkio valittavana,
joka voidaan laittaa jonon jatkoksi.
n! kutsutaan n:n kertomaksi, joka on n, n-1,...,2,1 tulo
eli 4! = 4 × 3 × 2 × 1
Tuloperiaatteen perusteella n:n alkion järjestysten
lukumäärä, jota kutsutaan permutaatioiksi, on
n! = n× (n-1) × ... × 2 × 1
Luvun 0 kertomaksi määritellään 0!
= 1, koska 0-alkioisten joukon eli tyhjän joukon alkiolla on vain
yksi järjestys.
|
1.3.2.Kuinka monella tavalla ? - järjestysten
lukumäärä. Kotitehtävien tekeminen taululle.
Opiskeljan ryhmässä on neljä poikaa ja
kolme tyttöä. Kotitehtävien tekijät taululle arvotaan.
Millä todennäköisyydellä kaikki pojat pääsevät
ensin taululle ja tytöt sen jälkeen ? |
Ratkaisu 1.3.2.
Alkeistapauksiksi valitaan kaikki taululle meno järjestykset
eli
1. taululle menijälle on 7 vaihtoehtoa,
2. taululle menijälle 6 vaihtoehtoa,
... ja
7. taululle menijälle on enää yksi vaihtoehto.
Järjestysten lukumääräksi saadaan
siis 7! = 7 * 6 * 5 * 4 * 3* 2 * 1 = 5 040, jotka kaikki alkeistapaukset
ovat yhtä todennäköisiä.
Suotuisia alkeistapauksia ovat ne, joissa pojat ovat
ensin taululla ja sen jälkeen tulevat tytöt eli
1.taululle menijälle on 4 vaihtoehtoa (poika),
2.taululle menijälle 3 vaihtoehtoa (poika),
3.taululle menijälle 2 vaihtoehtoa (poika),
4.taululle menijälle 1 vaihtoehto,
5.taululle menijälle 3 vaihtoehtoa (tyttö),
6.taululle menijälle 2 vaihtoehtoa (tyttö)
ja
7.taululle menijälle 1 vaihtoehtoa (tyttö).
Eli suotuisten järjestysten lukumääräksi
tuloperiaatteen perusteella tulee
4 * 3 * 2 * 1 * 3* 2 * 1 = 4! * 3! = 144
eli kysytty todennäköisyys
P({pojat ensin ja sitten tytöt}) = (4! * 3!) : 7! = 144 : 5 040 *
0,029 |
1.3.3. Osajoukkojen lukumäärä. Bridge-illan
kokoonpanot
Bridge-iltaan on kutsuttu 8 henkilöä, mutta
kahdelle kutsutulle tuli tärkeämpää tekemistä
eivätkä siten päässeet peli-iltaan. Kerralla bridgepeliin
voi osallistua 4 henkilöä, kuinka monta eri kokoonpanoa peliin
saadaan mukaan? |
Ratkaisu 1.3.3.
Valitaan pelaajat tulleiden 6 henkilön {a, b, c,
d, e, f} joukosta
1.pelaajan vaihtoehtoja on 6 .
2.pelaajan valintaan mahdollisuuksia on 5,
3.kolmannen pelaajan valintaan 4 ja
4.pelaajan valintaan 3 vaihtoehtoa.
Kuuden henkilön ryhmästä voidaan muodostaa
6 * 5 * 4 * 3 = 360 erilaista neljän henkilön
kokoonpanoa.
Eri kokoonpanot voivat muodostua samoista pelaajista
eli samat pelaajat voivat tulla valituksi usealla eri tavalla esimerkiksi
a,b,d,e tai d,a,b,e tai e,d,b,a jne.
Samoista neljästä pelaajasta voidaan muodostaa
järjestyksiä
4! = 4 * 3 * 2 * 1 = 24 erilaista.
Kokoonpanojen lukumäärä 360 on 24-kertaisena,
joten erilaisten kokoonpanojen lukumäärä on
360 : 24 = 15.
Tämä voidaan laskea käyttäen apuna
binomikerrointa eli
 |
1.3.4. Kuvakorttien todennäköisyys
Otetaan tavallinen 52 pelikortin pakka. Mikä on
todennäköisyys, että ottamalla satunnaisesti
a) kortti, saadaan kuvakortti tai ässä, jota
ei lasketa kuvakortteihin,
b) kaksi korttia, saadaan kaksi ruutua tai kaksi ässää
? |
Ratkaisu 1.3.4
a) kuvakortti tai ässä
Alkeistapauksia yhden kortin ottamiselle on 52 kappaletta.
Suotuisia tapauksia, tapahtumalle joko kuvakortti tai ässä, on
kuvakortille 12 ja ässälle 4. Koska ässiä ei lueta
kuvakortteihin, suotuisia alkeistapauksia on n(suotuisat alkeistapaukset)
= 12 + 4.
Tällöin todennäköisyys, että
saadaan joko kuvakortti tai ässä, jota ei lueta kuvakortteihin
on

b) kaksi ruutua tai kaksi ässää
Alkeistapauksia on nyt kaikki 52:sta kortista otetut
2 kortin jonot eli ensimmäinen kortti voidaan valita 52:sta kortista
ja toinen kortti 51:sta kortista. Alkeistapauksia on kaikkiaan

Ruuduille suotuisia tapauksia ensimmäiselle kortille
on 13 kappaletta eli se voidaan valita 13 ruutukortin joukosta ja toinen
kortti voidaan valita loppujen 12 ruutukortin joukosta. Suotuisia alkeistapauksia
on siis kaikkiaan

Ässeille suotuisia tapauksia ensimmäisellä
kortilla on 4 ja toisella kortilla 3 eli

Korttipakkaan kuuluu myös ruutuässä, joka
on sekä ruutu että ässä. Otettaessa suotuisiin tapauksiin
mukaan kaikki ruudut ja kaikki ässät, tulee ruutuässä
molempiin eli kahteen kertaan mukaan. Tällöin suotuisien alkeistapauksien
joukosta on poistettava "toinen" ruutuässä.
Todennäköisyys, että saadaan molemmilla
korteilla ruutu tai molemmilla korteilla ässä, on todennäköisyys
saada kaksi ruutua tai todennäköisyys saada molemmilla ässä
poislukien yksi ruutuässä eli

Todennäköisyyslaskennan yhteenlaskusääntö
on kahden tapahtuman A ja B tapauksessa

Kun tapahtumat ovat erillisiä eli tapahtumat A ja
B ovat toisensa poissulkevia eli A:lla ja B:lla ei ole yhteisiä alkeistapauksia,
niin poissulkevien tapahtumien yhteenlaskusäännöksi saadaan

Yleisessä muodossa yhteenlaskusääntö
erillisille tapahtumille on

|
|
Ehdollinen todennäköisyys
Ehdollista todennäköisyyttä tarvitaan silloin,
kun tieto toisen tapahtuman esiintymisestä vaikuttaa tutkittavan tapahtuman
todennäköisyyteen. Esimerkiksi, jos valitaan umpimähkään
yksi maailman 4 miljardista ihmisestä, on todennäköisyys
sille, että hän on suomalainen noin
1/1 000. Jos valinnan tapahduttua paljastetaan tieto,
että valittu henkilö lukee juuri tätä monistetta, on
todennäköisyys olla suomalainen olennaisesti suurempi. Ehdollistaja
siis muuttaa perusjoukkoa. Kun tunnetaan tapahtuman A ja ehdollistajan
B todennäköisyydet ja yhteistodennäköisyys, voidaan
ehdollinen todennäköisyys laskea kaavasta

Kun kaavasta ratkaistaan P(A ja B), saadaan kertolaskusäännölle
yleistys eli A:n ja B:n välistä riippumattomuutta ei tarvitse
olettaa käytettäessä kaavaa
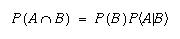
Riippumattomuus määritelläänkin
ehdollisen todennäköisyyden avulla: Tapahtumat A ja B ovat toisistaan
riippumattomia, jos ja vain jos
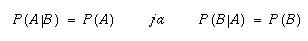
|
|
| 2. luku TODENNÄKÖISYYSJAKAUMA |
Satunnaismuuttuja
Satunnaismuuttujat
ovat empiiristen muuttujien
matemaattisia vastineita. Niiden avulla voidaan empiirisen muuttujan arvoissa
esiintyvä vaihtelu ilmaista matemaattisin termein.
Satunnaismuuttuja liittää
kaikkiin mahdollisiin alkeistapauksiin todennäköisyyden. Satunnaismuuttujan
X todennäköisyysjakauma muodostuu
· muuttujan
arvoista xi
· arvoihin liittyvistä
todennäköisyyksistä pi
|
Diskreetti satunnaismuuttuja
Satunnaismuuttujaa, joka
saa vain tiettyjä arvoja (esim. kokonaislukuja), sanotaan epäjatkuvaksi
eli diskreetiksi satunnaismuuttujaksi. Vastaavasti jatkuva satunnaismuuttuja
saa mitä tahansa reaalilukuarvoja tietyllä välillä. |
Tiheysfunktio
Todennäköisyydet
pi voidaan kuvitella massaksi, jonka arvo on yksi ja jakaantuu eri X:n
arvojen kesken sen mukaan, mikä kunkin arvon todennäköisyys
on. Jos kyseessä on epäjatkuva satunnaismuuttuja, keskittyy todennäköisyysmassa
yksittäisten xi arvojen kohdalle. Todennäköisyysmassan jakauman
ilmoittavaa funktiota sanotaan
tiheysfunktioksi f(x).
Epäjatkuvan satunnaismuuttujan
tiheysfunktio ilmoittaa kunkin tulosmahdollisuuden xi todennäköisyyden.
Esimerkiksi rahanheitossa tulosmahdollisuuksia on x1=kruuna ja x2=klaava.
Molempien tulosvaihtoehtojen todennäköisyys on sama eli f(x1)=0.5
ja f(x2)=0.5. Rahanheiton tuloksen X tiheysfunktio saa siis X:n arvolla
x1 (kruuna) arvon 0.5 ja X:n arvolla x2 (klaava) arvon 0.5.
Vastaavasti jatkuvan satunnaismuuttujan
tiheysfunktiota ei voida määritellä pisteittäin. Koska
jatkuva satunnaismuuttuja voi saavuttaa äärettömän
monta arvoa määrittelyvälillään, on yhden pisteen
todennäköisyys nolla. Jatkuvan satunnaismuuttujaan liittyviä
todennäköisyyksiä käsitellään välien
avulla (joka johtaa summauksien korvaamisen integroinnilla).
|
Kertymäfunktio
Satunnaismuuttujan X kertymäfunktio
F(x) määritellään kaavasta:
F(x) = P( X < x )
Kertymäfunktion arvo
kohdassa x ilmaisee sen, millä todennäköisyydellä satunnaismuuttuja
X saa arvon, joka on korkeintaan x.
F(x) on funktio, jonka arvo
kohdassa x ilmoittaa tapauksen

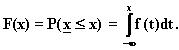
Huom! Todennäköisyys
on kertymäfunktion arvojen erotus,
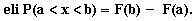
Satunnaismuuttujalle X voidaan
määrätä tunnuslukuja eli parametreja sen todennäköisyysjakaumasta.
Tunnusluvut kuvaavat jotain jakauman ominaisuutta, esimerkiksi jakauman
paikkaa kuten odotusarvo E(X) (tai m) tai sen leveyttä, kuten varianssi
D2(X) tai Var(X) (tai s2).
|
| Odotusarvo
Epäjatkuvan jakauman
odotusarvo (expected) saadaan kaavasta
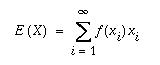
ODOTUSARVO on jakauman
tunnusluku, joka kertoo "odotettavissa" olevan (engl. Expected value) arvon.
Usein sitä sanotaan myös jakauman keskiarvoksi.
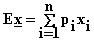
E1 Nopanheiton pistelukujen
odotusarvo saadaan helposti em. kaavalla:
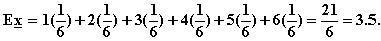
Varianssi mittaa jakauman
keskimääräistä poikkeamaa odotusarvosta ja epäjatkuvan
jakauman varianssi lasketaan kaavasta

VARIANSSI on jakauman hajontaluku,
joka luonnehtii arvojen jakautumista keskiarvon (odotusarvon ympärille).
Varianssin laskemiseksi pitää ensin laskea odotusarvo.

Nopanheiton pistelukujen
varianssi on
 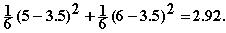
Vastaavasti jatkuvalle satunnaismuuttujalle
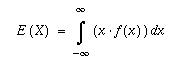
|
|
Todennäköisyyslaskennassa
voidaan ajatella olevan kolme tasoa:
· mikrotaso, joka
tarkoittaa yksittäisiä todennäköisyyksiä
· mesotaso koostuu
todennäköisyysjakaumista
· makrotaso tarkoittaa
todennäköisyysjakaumista laskettuja tunnuslukuja
Tilastollisessa päätöksenteossa
käytetään teoreettisia jakaumia perusjoukon (joukon, johon
tutkimuksen tulos yleistetään) mallina. Otoksesta saadun empiirisen
jakauman oletetaan olevan peräisin tästä todennäköisyysjakaumasta
ja empiirisen jakauman perusteella pyritään tekemään
johtopäätöksiä perusjoukon mallina olevasta teoreettisesta
todennäköisyysjakaumasta
a) estimoinnilla,
perusjoukon parametria arvioidaan otoksesta lasketulla tunnusluvulla.(esim.
odotusarvoa arvioidaan keskiarvolla)
b) hypoteesin testauksella,
perusjoukon parametreihin liittyvä hypoteesi ja tutkitaan tukeeko
saatu havaintoaineisto hypoteesia.
|
Esimerkkejä todennäköisyysjakaumista
Esimerkki 1.
Heitetään
kahta noppaa ja tutkitaan silmälukujen summan todennäköisyysjakaumaa,
eli määrätään todennäköisyydet P(X=2),
P(X=3), P(X=4),...,P(X=12), missä X on satunnaismuuttuja, joka ilmaisee
noppien silmäluvun summan.
Nopat ovat erillisiä
ja toisistaan riippumattomia, joten voidaan nimetä toinen noppa 1.
nopaksi ja toinen noppa 2. nopaksi. Noppien silmäluvuista ja niiden
summasta voidaan esittää taulukko, jossa vaakasuoraan esitetään
1. nopan tulos ja pystysuoraan 2. nopan tulos sekä ruudukon sisällä
on silmälukujen summa.
Taulukossa on esitetty
kaikki mahdolliset tulokset eli alkeistapausavaruus.

Kaikki silmälukuparit
ovat yhtä todennäköisiä. Huomaa, että esimerkiksi
pari {5,6} voidaan saada kahdella tavalla: 1. noppa on 5 ja 2. noppa on
6 sekä 1. noppa on 6 ja 2. noppa on 5, kun taas samat numerot voidaan
saada vain yhdellä tavalla: esimerkiksi pari {5,5} voidaan saada vain
siten, että 1. noppa on 5 ja 2. noppa on 5.
Symmetrisyyden perusteella
saadaan määriteltyä nopanheiton silmäluvun todennäköisyysjakauma
klassisen todennäköisyyden avulla: lasketaan suotuisten vaihtoehtojen
määrä ja jaetaan se kaikkien vaihtoehtojen määrällä.
Kaikkaan ruutuja taulukossa on 6*6 = 36, joka on kaikkien vaihtoehtojen
määrä.
Todennäköisyysjakauma
voidaan esittää myös vaakasuorana taulukkona.

Kertymäfunktio samasta
jakaumasta saadaan summaamalla tiheysfuntion pistetodennäköisyyksiä,
eli kaavalla
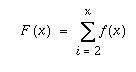
Kertymäfunktio
Todennäköisyysjakauman
odotusarvo.
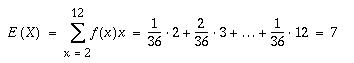
Tämä on tulkittavissa
siten, että toistettaessa noppaparin heittoa, saadaan silmälukujen
summan keskiarvoksi 7.
Esimerkkejä kuinka
tiheys- ja kertymäfunktiota voidaan käyttää apuna todennäköisyyslaskuissa:
a) Millä
todennäköisyydellä silmälukujen summa on 6, 7 tai 8
?
f(6) + f(7) + f(8) = 5/36
+ 6/36 + 5/36 = 16/36
tai P(5 < X < 9) =
F(8) - F(5) = 26/36 - 10/36 = 16/36
b) Mitä silmälukua
pienempiä on 1/3 tuloksista ?
Kun lasketaan kertymäfunktiosta
murtoluvut likiarvoiksi saadaan
F(5) = 10/36 = 0.278 ja
F(6) = 15/36 = 0.417. Kolmasosa 1/3 = 0.333.
Vastaukseksi saadaan, että
1/3 jakaumasta on alle 7.
Esimerkki 2
Kolme kenttäbiologia
etsii rämeiköltä mäkihyppysammakoita toisistaan riippumattomasti.
Mäkihyppysammakon havaitsemistodennäköisyys yhdellä
kenttäbiologilla on 0.3. Määrää todennäköisyysjakauma
sille, kuinka moni kenttäbiologi havaitsee mäkihyppysammakon.
Alkeistapausavaruus on {0,1,2,3}
eli 0 vastaa sitä, että yksikään ei havaitse sammakkoa
ja 3 vastaa sitä, että kaikki havaitsevat.
Nimetään havainnoitsijat
kirjaimilla A, B ja C. Olkoon X satunnaismuuttuja, joka yhdistää
havaitsijoiden lukumäärän vastaaviin todennäköisyyksiin.
P(X=0) = P{A ei havaitse
ja B ei havaitse ja C ei havaitse}
= P{A ei havaitse}·P{B
ei havaitse}·P{C ei havaitse}
= (1 - 0.3)(1-0.3)(1-0.3)
= 0.73 = 0.343
P(X=1) = P{A havaitsee ja
B ei havaitse ja C ei havaitse} + P{A ei havaitse ja B havaitsee ja C ei
havaitse} + P{A ei havaitse ja B ei havaitse ja C havaitsee}
= 0.3·(1-0.3)·(1-0.3)
+ (1-0.3)·0.3·(1-0.3) + (1-0.3)·(1-0.3)·0.3
= 0.441
P(X=2) = 3 · 0.3
· 0.3 · (1-0.3) = 0.189
P(X=3) = 0.33 = 0.027
Kaikkien tapausten yhteenlaskettu
todennäköisyys
P(X=0)+P(X=1)+P(X=2)+P(X=3)
= 0.343 + 0.441 + 0.189 + 0.027 = 1.
Todennäköisyysjakauman
tiheysfunktiosta ja kertymäfunktiosta voidaan esittää seuraavat
kuviot tiheysfunktiosta

ja kertymäfunktiosta
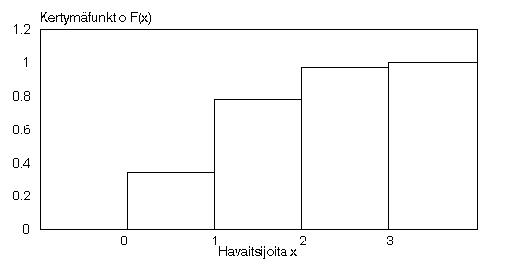
(pystyviivat eivät kuulu
kuvioon!).
Jakauman odotusarvoksi saadaan

Tämä on tulkittavissa
siten, että koetta toistettaessa havaitsijoiden lukumäärän
keskiarvoksi saadaan 0.9.
Esimerkki 3
Tutkitaan koe-eläimen
elinaikaa tutkimuksessa (esim. hyönteinen). Maksimielinaika on 1 tunti
ja kuolemisen todennäköisyys on sama koko tutkimuksen ajan. Satunnaisesti
poimitun koe-eläimen iän todennäköisyysjakauma on määrittelyn
mukaan seuraavan kaltainen.
Määrätään
a, kun tiedetään, että tiheysfunktion pinta-ala = 1 (eli
kaikkien mahdollisuuksien yhteenlaskettu tn = 1). Kolmion pinta-alan kaavasta
saadaan
(1 · a) / 2 = 1 <=>
a = 2
Pisteiden (0,2) ja (1,0)
kautta kulkevan suoran yhtälö on muotoa f(x) = 2 - 2x, joten
tiheysfunktioksi saadaan
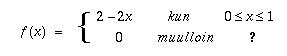
Kertymäfunktio määrittelyvälillä
0<x<1 saadaan tiheysfunktion integraalina:
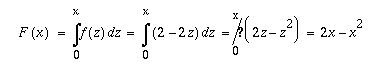
Näet funktion graafisen
estyksen klikkaamalla funktiota.
Elinajan odotusarvoksi saadaan

Odotusarvo on tulkittavissa
koe-eläinten keskimääräiseksi eliniäksi.
Binomijakauma (diskreetti jakauma)
Heitetään rahaa.
Tulosmahdollisuudet ovat kruuna ja klaava, joiden todennäköisyydet
yhdessä heitossa ovat 0.5 ja 0.5. Toistetaan rahanheitto k kertaa
ja mielenkiinnon kohteena on kuinka monta klaavaa saadaan.
Yhdessä heitossa (k=1)
nollan klaavan tn=0.5 ja yhden klaavan tn=0.5.
Kahdessa heitossa (k=2)
: aina heitoista saadaan 1/2 * 1/2 = 1/4
nolla klaavaa voidaan saada
vain yhdellä tavalla: (kr, kr)
joten todennäköisyys
on 1/4
yksi klaava voidaan saada
kahdella tavalla: (kl, kr), (kr, kl)
joten todennäköisyys
on 2/4 = 1/2
kaksi klaavaa voidaan saada
vain yhdellä tavalla: (kl, kl)
joten todennäköisyys
on 1/4
Kolmessa heitossa (k=3):
edelleen 1/2 * 1/2 * 1/2 = 1/8
nolla klaavaa saadaan vain
yhdellä tavalla: (kr, kr, kr)
joten tn = 1/8
yksi klaava saadaan kolmella
tavalla: (kl, kr, kr),(kr, kl, kr),(kr, kr, kl)
joten tn = 3 * 1/8 = 3/8
kaksi klaavaa saadaan kolmella
tavalla: (kl, kl, kr),(kl, kr, kl),(kr, kl, kl)
joten tn = 3 * 1/8 = 3/8
kolme klaavaa saadaan yhdellä
tavalla: (kl, kl, kl)
joten tn = 1/8
Kun merkitään
p:llä onnistumisen todennäköisyyttä yhdessä toistokokeessa
(rahanheitossa = 1/2) ja toistojen lukumäärää n:llä,
saadaan kombinatoriikan perusteella binomijakauman tiheysfunktioksi
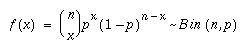
Huomaa, että binomijakaumassa
onnistumisen todennäköisyyden ei tarvitse olla 0.5, vaan se saa
olla mitä hyvänsä nollan ja yhden väliltä.
Binomijakauma toimii dikotomisten
muuttujien mallina, kun tutkitaan esiintyykö jotain asiaa vai ei (esim.
sairautta). Toistojen lukumäärää n vastaa havaintojen
määrä ja arvioitavana on yhden henkilön sairastumisalttius
p, kun otoksesta saatu sairaiden lukumäärä on k.
Binomijakauma on tilastotieteessä
tärkein epäjatkuva jakauma. Muita epäjatkuvia teoreettisia
jakaumia ovat mm. Multinomijakauma, Poissonjakauma, Hypergeometrinen
jakauma ja Geometrinen jakauma.
Normaalijakauma(jatkuva
jakauma)
Normaalijakauma ja siitä
johdetut jakaumat ovat tärkeimmät tilastotieteessä käytetyt
jakaumat. Hyvin monet asiat (muuttujat) luonnossa noudattavat normaalijakaumaa
tai ainakin liki normaalijakaumaa. Satunnaismuuttujaa sanotaan normaalijakautuneeksi,
jos sen tiheysfunktio on muotoa
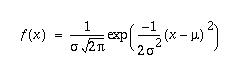

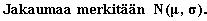

Todennäköisyyksiä
laskettaessa jakauma on normitettava
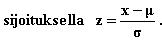
Esimerkki.
Määritä
jakaumalle N(5,1) todennäköisyys



Ilmoita vastauksesi
4 desimaalin tarkkuudella.
Ratkaisu
a) Todennäkösyys
P(x <10)
muuntuu normeeratun jakauman
todennäköisyydeksi muunnoskaavalla
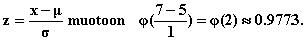

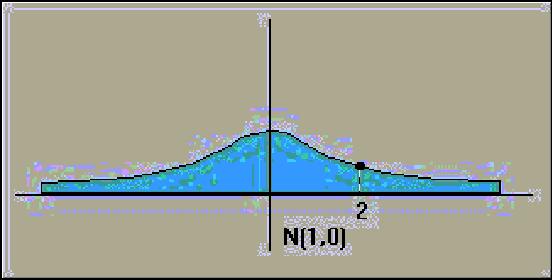
b) Todetaan ensin,
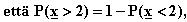
josta se muuntuu muunnoskaavalla

Tästä saadaan
suoraan laskimella tulokseksi

Jos joudutaan käyttämään
taulukkoa, kirjoitetaan ensin
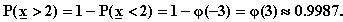

c) Kysytty todennäköisyys
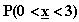
muunnetaan ensin muunnoskaavalla
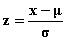
kertymäfunktion erotukseksi
muotoon
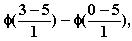

Tälle saadaan suoraan
laskimella arvo 0.0227.
Jouduttaessa käyttämään
taulukkoa kirjoitetaan ensin

josta tulee vastaukseksi
0.0227 .
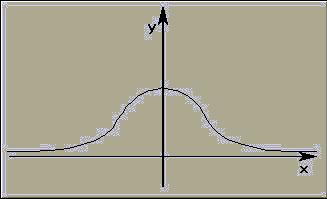
Normaalijakauma on muodoltaan
yllä olevan näköinen, kun se on normitettu, eli odotusarvo
= 1 ja keskihajonta = 0.
Tiheysfunktio on silloin

Koska sitä ei voida
integroida alkeisfunktioiden avulla, arvot luetaan taulukosta tai laskimesta.
Esimerkki
Jakauma on muotoa N(0,1),
eli normitettu normaalijakauma.
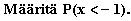
Ratkaisu
Kysytty todennäköysssys
saadaan suoraan laskimesta, mutta taulukon käyttäjän osattava
käyttää Gaussin käyrää apuna seuraavalla
tavalla:
Piirretään käyrä
ja varjostetaan sen ja x-akselin väliin jäävä alue
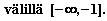
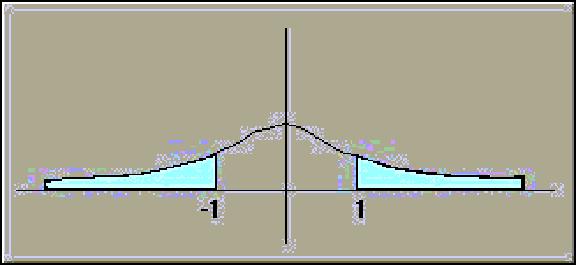
Todetaan, että alue
välillä
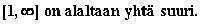
Siis kysytty todennäköisyys
saadaan siten,

eli luvusta yksi vähennetään
kertymäfunktion arvo kohdassa 1, joka saadaan taulukosta. Tulokseksi
saadaan

Vastaavalla tavalla lasketaan
kaikki muutkin todennäköisyydet, jos joudutaan käyttämään
taulukkoa.
Tiheysfunktiossa esiintyvä
parametri m on normaalijakauman odotusarvo ja s2 sen varianssi. Normaalijakauman
tiheysfunktiosta ei tarvitse käsin laskea arvoja, sillä standardoidun
normaalijakauman kertymäfunktion arvoja ( F(z) = P(Z < z) ) on
taulukoitu normaalijakaumaan perustuvaa päättelyä varten.
Standardoidun normaalijakauman odotusarvo on m = 0 ja varianssi s2 = 1.
Muuttuja, joka noudattaa
normaalijakaumaa parametrein m, s2, saadaan standardoitua, eli noudattamaan
standardoitua normaalijakaumaa, muunnoskaavan
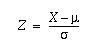
avulla, jossa uusi muuttuja
Z noudattaa standardoitua normaalijakaumaa.
Tunnuslukuja (statistics)
Tunnusluvut ilmoittavat
jonkin muuttujan ominaisuuden. Tunnusluvut voidaan jakaa keski-, hajonta-
ja muihin tunnuslukuihin. Keskiluvut kuvaavat muuttujan jakauman sijaintia,
hajontaluvut ilmoittavat jakauman "hajaantumisen" ja muut tunnusluvut tutkivat
muita jakauman ominaisuuksia, kuten vinoutta ja huipukkuutta.
Mikäli havaintoaineisto
on valmiiksi luokiteltu, lasketaan keskiarvoluokitellusta muuttujasta
luokkakeskusten avulla (luokkakeskusten frekvensseillä painotettu
keskiarvo):
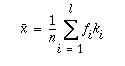
missä fi on
luokan i frekvenssi ja ki saman luokan luokkakeskus sekä l
on luokkien lukumäärä.
Vastaavasti geometrinen
keskiarvo, joka voidaan laskea vain suhdeasteikon muuttujasta saadaan
kaavasta
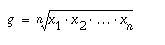
Mediaani (md)
(median) voidaan määrätä suuruusjärjestykseen
järjestetystä aineistosta. Mediaani on keskimmäinen havaintoarvo,
eli arvo, jota suurempia ja pienempiä havaintoja on yhtä monta.
Mikäli havaintoja on parillinen määrä, ei keskimmäistä
havaintoarvoa ole olemassa. Tällöin mediaaniksi voidaan valita
jompi kumpi keskimmäisistä havaintoarvoista tai näiden keskiarvo.
Mediaania ei voida määritellä luokitteluasteikon muuttujasta.
Fraktiilit ovat prosenttisummafrekvenssin
perusteella määrättyjä pisteitä jakaumasta. Mediaani
on 50 %:n fraktiili. Fraktiili nimetään sen mukaan, kuinka monen
osaan jakauma jaetaan, esimerkiksi
- kvartiilit
25
%, 50 % (mediaani) ja 75 %
- tertiilit 33.3
% ja 66.7 %
- kvintiilit 20 %,
40 %, 60 % ja 80 %
- desiilit 10%, 20%,
30%, 40%, 50%, 60%, 70%, 80% ja 90%.
Hajontalukuja
Käytetyin hajontaluku
on keskihajonta (standard deviation), joka ilmoittaa havaintoarvojen
hajaantumisen keskiarvon ympärille. Seuraava kaava kertoo millainen
tunnusluku keskihajonta on
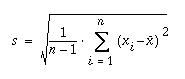
Käsin laskettaessa
keskihajonta on helpoin laskea siten, että ensin lasketaan havaintojen
summa ja neliösumma ja nämä sijoitetaan seuraavaan kaavaan

Luokitellulle muuttujalle
keskihajonta lasketaan korvaamalla havaintoarvot luokkakeskuksilla. Kun
luokan i frekvenssiä merkitään fi:llä ja luokkakeskusta
ki:llä, saadaan keskihajonta seuraavasta kaavasta:
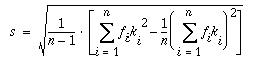
Keskihajonta on järkevä
hajontaluku vain välimatka- ja suhdeasteikon muuttujille.
Varianssi (variance)
on keskihajonnan neliö s2.
Variaatiokerroin V
= s / x on suhteellinen keskihajonta. Sillä saadaan eri suuruusluokkaa
olevien muuttujien hajonnat vertailukelpoisiksi. Variaatiokerroin voidaan
laskea vain suhdeasteikon muuttujille.
Keskiarvon keskivirhe
(standard error of mean) kuvaa keskiarvon luotettavuutta. Käytetään
usein keskiarvokuvioissa ja taulukoissa. Keskivirheen käsite liittyy
estimointiin.
Vaihteluvälin pituus
on
suurimman havaintoarvon ja pienimmän havaintoarvon välinen erotus.
Jos suuruusjärjestykseen asetettua havaintoaineistoa merkitään
x(1), x(2),...,x(n), saadaan vaihteluvälin pituudelle kaava d = x(n)
- x(1).
Vaihteluväli (range)
voidaan
esittää jo järjestysasteikon muuttujasta. Tällöin
ilmoitetaan suurin ja pienin
havaintoarvo R = (x(1) ,
x(n)).
HARJOITUSTEHTÄVIÄ
1.Suoran y = kx - 2 kulmakerroin
määritetään nopanheitolla. Millä todennäköisyydellä
suora kohtaa

2. Piste S valitaan sattumanvaraisesti
ympyränsektorista, jonka keskuskulma on 120 astetta. Millä todennäköisyydellä
se tulee valittua ko. sektorin sisään piirretystä ympyrästä
?
3. Aloitteleva mäkihyppääjä
kaatuu keskimäärin joka kymmenennen hyppynsä. Hän hyppää
kuusi harjoitushyppyä. Millä todennäköisyydellä
hän kaatuu ainakin kerran ?
4. Ryhmän 20 opiskelijasta
vain 16 on laskenut tietyn kotilaskun. Opettaja valitsee arpomalla 3 laskijaa.
Millä todennäköisyydellä mukaan tulee ainakin yksi,
joka ei ole laskenut tuota tehtävää ?
5. Kolme ruotsinkielistä
ja viisi suomenkielistä kirjaa asetetaan kirjahyllyyn. Kuinka monella
eri tavalla kirjat voidaan asettaa hyllyyn, kun vaatimuksena on se, että
samankielisten on oltava vierekkäin ?
6. Kuinka monella eri tavalla
9 videokasettia voidaan laittaa kirjahyllyyn, kun tietyt kaksi kasettia
eivät saa joutua
vierekkäin ?
7. Monivalintakokeessa 12
kysymystä, joista kussakin on neljä eri vaihtoehtoa ja yksi vaihtoehto
on oikea. Hyväksyttyyn suorituksen vaaditaan vähintään
puolet oikein. Opiskelija tietää vastauksen varmuudella neljään
kysymykseen, mutta muut hän joutuu arvaamaan. Laske tn, että
hän selviytyy tentistä.
8. Olkoon z:lla jakauma N(0,1).
Laske
 '
' 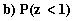 '
' 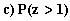 .
.

10. Älykkyysosamäärällä
on jakauma N(100,152). Millä todennäköisyydellä satunnaisesti
valitun henkilön älykkyysosamäärä on välillä
[91,121] ?
11. Falunissa 50 km hiihtokilpailu
noudatti likimain normaalijakaumaa odotusarvolla 2 t 30 min ja keskihajonnalla
10 min. Millä todennäköisyydellä hiihtäjältä
kuluu aikaa a) vähintään 2 t 50 min ? b) enintään
2 t 20 min ?
12. Normaalijakauman varianssi
on 6.25 ja odotusarvo 8. Määritä a,

13. Oletetaan, että
eräässä kunnassa syntyy ensi vuonna 60 lasta. Lasten sukupuolet
ovat toisistaan riippumattomia,
ja pojan syntymistodennäköisyys
on 0,513.
Mitä jakaumaa tyttöjen
ja poikien lukumäärät noudattavat ?
Mikä on poikien ja
mikä tyttöjen lukumäärän odotusarvo ?
Millä todennäköisyydellä
syntyy täsmälleen yhtä monta tyttöä ja poikaa
?
(Yo K99).
14. Erään jakauman
tiheysfunktio on määritelty siten, että

a) Mikä jakauma on
kyseessä ?
b) Määritä
K
c) Laske varianssi
d) Määritä
jakauman kertymäfunktio.
15. Piilastuja valmistetaan
tehtaassa, jolloin todennäköisyys,
että tuote on viallinen
on 15 %. Tehdas valmistaa 800 piilastua.
Millä todennäköisyydellä
alle 105 lastua on viallisia ?
Käytä normaalijakaumaa
arvioidessa binomijakaumaa siten,
että eli normaalijakaumalle
saadaan,
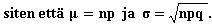
Parametrit n, p ja q ovat
binomijakaumasta.
Ilmoita vastauksesi prosentteina
yhden desimaalin tarkkuudella.
16. Espanjankielen kuuntelukokeessa
jokaisella kysymyksellä
on neljä vastausvaihtoehtoa, joista
vain yksi on oikea.
Yhden kysymyksen sanamuoto on niin
epäselvä,
että kokelas joutuu arvaamaan.
Millä todennäköisyydellä
enintään puolet kokelaista arvaa oikein tämän kysymyksen
kohdalla ?
Tenttiin osallistuu kuusi opiskelijaa.
17.
VASTAUKSIA
1. Suoran ja paraabelin yhteiset
pisteet löytyvät yhtälöparista,
joten muodostetaan ensin
yhtälöpari

Sijoitusmenetelmän
käyttö tuottaa

Tällä on yksi
tai kaksi ratkaisua,

Tämän ratkaisu
on

Nopan pisteluvuista voivat
tulla kysymykseen 3, 4, 5 tai 6.
Siis kysytty todennäköisyys
on

2: Sektorin ala on

Sektorin sisään
piirretyn ympyrän säteen laskemiseksi käytetään
erikoiskolmiota oheisen kuvion mukaisesti. Silloin saadaan yhtälö

josta sektorin sisään
piirretyn ympyrän säteeksi tulee

Tämä sievenee
laventamalla

Sisään piirretyn
ympyrän ala on silloin

Kysytty todennäköisyys
on nyt klassisen todennäköisyyden kaavan mukaisesti
(Voidaan puhua myös
geometrisesta todennäköisyydestä.)

Tämä supistuu
muotoon

josta saadaan laskimella
3-desimaalinen likiarvo P = 0.646.
3. Kaatumistodennäköisyys
on

Sana "ainakin" viittaa komplementtisäännön
käyttöön. Komplementtitapaus on se, ettei hän kaadu
lainkaan.
Tämän todennäköisyys
kuuden hypyn sarjassa on

Kysytty todennäköisyys
on silloin

4. Sana "ainakin" viittaa
komplementtisäännön käyttöön.
Komplementtitapaus on se,
että kaikki ovat laskeneet tehtävän.
Kolme laskijaa voidaan valita
16:sta

Kolme laskijaa valitaan
20:stä

Siis komplementtitapauksen
todennäköisyys on

Laskimella tämän
arvoksi tulee

Kysytty todennäköisyys
on silloin

5. Kolme kirjaa voidaan permutoida
3! ja viisi kirjaa 5! eri tavalla. Yksi suotuinen sarja (kuvio) voidaan
permutoida 3!5! eri tavalla.

Suotuisia sarjoja on 6 kpl.
Sen voi päätellä esim. siten, että siirretään
suomenkielisiä yksitellen ruotsinkielisten oikealle puolelle. Näin
ollen kaikkia mahdollisia tapoja järjestää kirjat vaaditulla
tavalla
on yhteensä 6*3!*5!
= 4320
6. Kaikki 9 kasettia voidaan
permutoida 9! eri tavalla. Edellisen tehtävän mukaisesti kasetit
voidaan järjestää vierekkäin
8*2!*7! eri tavalla siten,
että tietyt kaksi ovat
aina vierekkäin. Mutta näin ei saanut olla, joten kysyttyjä
tapoja on
9! - 8*2!*7! = 282240 kpl.
7. Opiskelijan on saatava
vähintään 6 oikeaa vastausta, joista jo 4 on varmoja. Hänen
on siis tiedettävä vähintään 2 oikein aikaisempien
oikeiden lisäksi. Sana "vähintään" johtaa käyttämään
komplementtisääntöä. Vaaditun tapauksen komplementti
on se, että opiskelija saa neljän oikean lisäksi 0 tai 1
oikein vastatessaan jäljellä olevaan 8 kysymykseen. Tämän
todennäköisyyden laskemiseksi käytetään binomitodennäköisyyden
kaavaa ja saadaan

Tämä sievenee
nopeasti muotoon

josta laskin antaa likiarvoksi
0.3671. Siis kysytty todennäköisyys on P = 1 - 0.3671 = 0.6329.
Vastaus on siis 3:lla desimaalilla P = 0.633.
8. a) Tarkastellaan Gaussin
käyrää
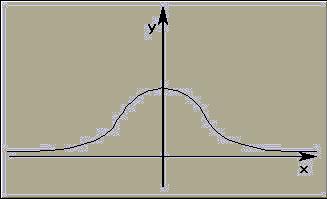
Viivoitettu alue on
tasan puolet koko alueesta, jonka ala on =1,


kuten laskin tai taulukko
antaa arvoksi.

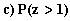
on komplementti todennäköisyydelle

10. Kysytty todennäköisyys

voidaan kirjoittaa normeeratun jakauman
avulla muotoon
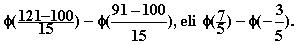
Tälle saadaan laskimella arvo 0.6449.
Jos joudutaan käyttämään
taulukkoa, kirjoitetaan erotus

ensin muotoon
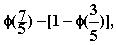
eli tästä edelleen muotoon
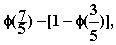
Käyttämällä taulukkoa
päädytään 3-desimaaliseen vastaukseen P = 0.645.
11. Olettamustiedot minuutteina
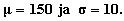
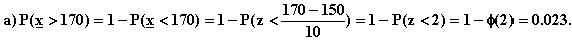
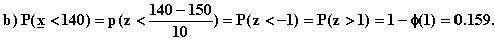
12. Keskihajonta on
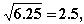
joten jakauma on tyyppiä N(8, 2.5).
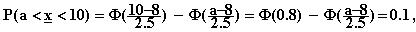
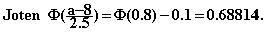
Etsitään ratkaisua yhtälölle
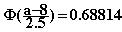
laskimen avulla. Silloin oltava

13. Kyseessä on binomijakauma Bin(n,
p), joka on poikien tapauksessa Bin(60, 0.513) ja tyttöjen Bin(60,
0.487).
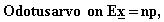
eli poikien määrän
odotusarvo on
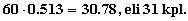
Vastaava tyttöjen määrän
odotusarvo on

Tyttöjä ja poikia syntyy yhtä
monta, jos poikia syntyy 30. Tämä lasketaan binomitodennäköisyyden
kaavalla ja saadaan
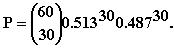
Laskin antaa vastaukseksi kolmella desimaalilla
P = 0.101.
14. a) Kyseessä on tasainen jakauma,
joka on erikoistapaus jatkuvasta jakaumasta.
b) Koko nollasta eriävä tapausavaruus
rajoittuu

Siis suoran y = K alle jäävän
suorakaiteen pinta-alan tulee olla = 1,

josta saadaan K = 2.
c) Varianssi on kaavan mukaan
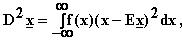
eli tässä tapauksessa on
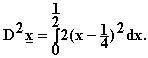
on tasaisella jakaumalla välin keskikohta,
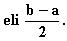
Kun integraali lasketaan, tulee
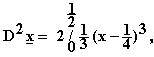
josta saadaan
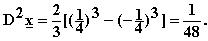
d) Kertymäfunktio on

eli tässä tapauksessa
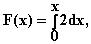
Integroinnin jälkeen on F(x) = 2x.
Kysytty kertymäfunktio koko tapausavaruudessa on
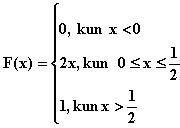
15. Kyseessä on binomijakauma, mutta
kysytyn todennäköisyyden laskeminen olisi tavattoman työlästä.
Onneksi binomijakaumaa voidaan likimääräisesti arvioida
(approksimoida) tehtävässä kerrotulla tavalla.
Lasketaan ensin binomijakauman odotusarvo
ja keskihajonta.
Suoraan kaavoja käyttämällä
saadaan


Kysytyn todennäköisyyden laskemiseksi
käytetään normaalijakaumaa
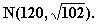
Tässä tapahtuu kyseinen approksimointi.
Lasketaan siis todennäköisyys

Siirtymällä normeerattuun jakaumaan
voidaan kirjoittaa
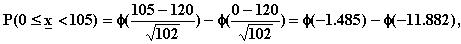
josta laskin antaa tulokseksi
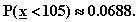
Siis 6.9 % todennäköisyydellä
piilastu on viallinen.
16.. Enintään puolet opiskelijoista
tarkoittaa tässä sitä,
että heitä on 0, 1, 2 tai 3.
On syytä käyttää komplementtisääntöä,
jolloin väärin arvanneita opiskelijoita
on 4, 5 tai 6.
Kysymyksessä on toistokoe,
joten käytetään binomitodennäköisyyden
kaavaa. Kysytty tn on

Tämä sievenee ensin muotoon

josta saadaan edelleen

17.
V