BIinomijakauma
Esim.1
Eräistä radioista on 40 % viallisia. Millä todennäköisyydellä
5 radion erässä on 2 viallista?
Ratkaisu
Kysymyksessä on
eräänlainen toistokoe. Jokainen radio vuorollaan todetaan
vialliseksi tai toimivaksi.
n = 5
Suotuisia tapauksia
(ironista kylläkin) ovat tässä tarkastelussa vialliset radiot.
k = 2
Epäsuotuisien tapausten
määrä
n û k = 3
Merkitään
V = viallinen, E = ehjä (toimiva)
viallisen todennäköisyys p = 0,4
ehjän tn. 1 û p = 0,6
Esiintymissarja, jossa
on kaksi viallista on silloin esim.
V V E E E
Tämän sarjan
todennäköisyys on
P ("VVEEE") = 0,4 · 0,4 · 0,6 · 0,6 ·
0,6 = 0,42 · 0,63
Mutta 5 radion sarjassa,
jossa on kaksi viallista, voivat vialliset kaksi sijaita muissakin järjestyksissä
| Kysytty tn. |
 |
0,35 = 35 % |
-
Varsinainen binomijakauma
saadaan, kun lasketaan todennäköisyydet kaikille mahdollisille
suotuisille määrille k
-
k = 5,
kaikki 5 vialllisia
P(A5) = 0,4 · 0,4 · 0,4
· 0,4 · 0,4 = 0,45 » 0,01 = 1 %
-
k = 4,
eli 4 vialllista ja 1 ehjä
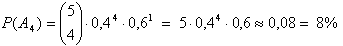
-
k = 3,
eli 3 vialllista ja 2 ehjää

-
k = 2,
eli 2 vialllista ja 3 ehjää

-
k = 1,
eli 1 vialllinen ja 4 ehjää

-
k = 0,
siis ei yhtään vialllista eli kaikki 5 ehjiä
P(A0) = 0,6 · 0,6 · 0,6
· 0,6 · 0,6 = 0,65 » 0,08 = 8 %
-
Kun lasketaan kaikki
todennäköisyydet yhteen, saadaan 101 %, jossa on 1 %-yksikkö
pyöristysvirhettä.
(Yhden desimaalin
tarkkuudella summa = 0,010 + 0,076 + 0,230 + 0,345 + 0,259 + 0,078 = 0,998
= 99,8%
pyöristysvirhe
enää 0,2 %-yksikköä)
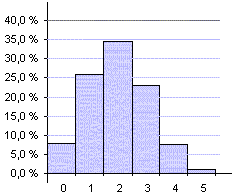
Esitetään vielä jakauma graafisesti
histogrammina |
 |
-
Odotusarvo E
eli todennäköisin arvo on k = 2
(korkein pylväs
kuvassa)
Odotusarvo E
lasketaan todennäköisyyksillä painotettuna keskiarvona
ja sen yleiskaava on
E = S
k · P(Ak)
E = 0 ·
0,08 + 1 · 0,26 + 2 · 0,35 + 3 · 0,23 + 4 ·
0,08 + 5 · 0,01 » 2
Erityisesti binomijakaumassa
odotusarvolle on helppo kaava
E = n
· p =5 · 0,4 = 2
|
