| Tehtävä 1.7. 4
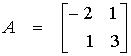
Ratkaisu
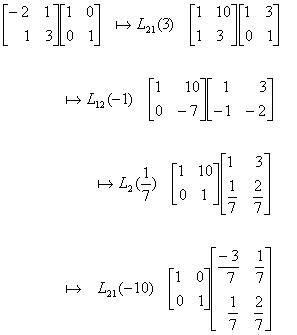
Vastaus
 , ,
Ratkaisu Matlabin avulla :
A = [-2 1; 1 3];
>> A^-1 ans =
-0.4286 0.1429
0.1429 0.2857
|
Tehtävä 1.7. 5
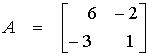
Ratkaisu
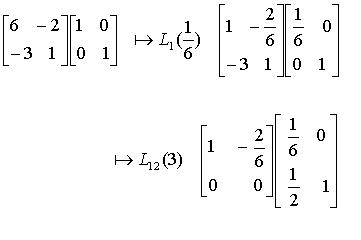
Vastaus
Matriisin viimeinen muunnettu muoto sisältää vaakarivin,
jolla on pelkkiä nollia. Tämä merkitsee sitä, että
muuntamista on turha jatkaa. Tälläisessä tapauksessa matriisilla
ei ole käänteismatriisia ja se on singulaarinen.
Ratkaisu Matlabin avulla :
>> A = [6 -2;-3 1]; >> A^-1
Warning: Matrix is singular to working precision
|
| Tehtävä 1.7. 6
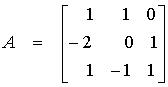
Ratkaisu

Vastaus
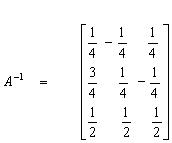
Ratkaisu Matlabin avulla :
A = [1 1 0; 2 0 1;1
-1 1]; >> A^-1
ans =
0.2500 -0.2500
0.2500
0.7500 0.2500
-0.2500
0.5000 0.5000
0.5000
|
Tehtävä 1.7.7

Ratkaisu

Vastaus
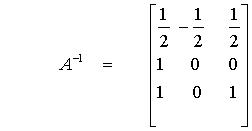
Ratkaisu Matlabin avulla :
A = [0 1 0; -2 0 1;0
-1 1]; >> A^-1
ans =
0.5000 -0.5000
0.5000
1.0000 0.0000
0.0000
1.0000 0.0000
1.0000 |