Tunnusluvutilmoittavat jonkin muuttujan ominaisuuden. Tunnusluvut voidaan jakaa keski-, hajonta- ja muihin tunnuslukuihin. Keskiluvut kuvaavat muuttujan jakauman sijaintia, hajontaluvut ilmoittavat jakauman "hajaantumisen" ja muut tunnusluvut tutkivat muita jakauman ominaisuuksia, kuten vinoutta ja huipukkuutta.
Mikäli havaintoaineisto on valmiiksi luokiteltu, lasketaan keskiarvoluokitellusta muuttujasta luokkakeskusten avulla (luokkakeskusten frekvensseillä painotettu keskiarvo):

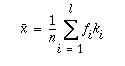
missä  fi on luokan i frekvenssi ja ki saman luokan luokkakeskus sekä l on luokkien lukumäärä.
 

Vastaavasti geometrinen keskiarvo, joka voidaan laskea vain suhdeasteikon muuttujasta saadaan kaavasta

 

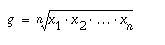
Mediaani  voidaan määrätä suuruusjärjestykseen järjestetystä aineistosta. Mediaani on keskimmäinen havaintoarvo, eli arvo, jota suurempia ja pienempiä havaintoja on yhtä monta. Mikäli havaintoja on parillinen määrä, ei keskimmäistä havaintoarvoa ole olemassa. Tällöin mediaaniksi voidaan valita jompi kumpi keskimmäisistä havaintoarvoista tai näiden keskiarvo. Mediaania ei voida määritellä luokitteluasteikon muuttujasta.
Fraktiilit ovat prosenttisummafrekvenssin perusteella määrättyjä pisteitä jakaumasta. Mediaani on 50 %:n fraktiili. Fraktiili nimetään sen mukaan, kuinka monen osaan jakauma jaetaan, esimerkiksi

- kvartiilit 25 %, 50 % (mediaani) ja 75 %
- tertiilit 33.3 % ja 66.7 %
- kvintiilit 20 %, 40 %, 60 % ja 80 %
- desiilit 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80% ja 90%.

Hajontalukuja

Keskihajonta (standard deviation)
Havaintoaineiston hajontaa kuvaa parhaiten keskihajonta . Keskihajonta on varianssin  neliöjuuri, joka on perusjakaumalle määritelty havaintojen keskiarvosta mitattujen poikkeamien neliöitten keskiarvojen raja-arvona: 

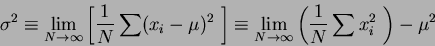
Keskihajonta  ilmoittaa havaintoarvojen hajaantumisen keskiarvon ympärille. Keskihajonta on järkevä hajontaluku vain välimatka- ja suhdeasteikon muuttujille.
 

Varianssi(variance) on keskihajonnan neliö.
 

Variaatiokerroin V = s / x on suhteellinen keskihajonta. Sillä saadaan eri suuruusluokkaa olevien muuttujien hajonnat vertailukelpoisiksi. Variaatiokerroin voidaan laskea vain suhdeasteikon muuttujille.

Keskiarvon keskivirhe (standard error of mean) kuvaa keskiarvon luotettavuutta. Käytetään usein keskiarvokuvioissa ja taulukoissa. Keskivirheen käsite liittyy estimointiin.

Vaihteluvälin pituuson suurimman havaintoarvon ja pienimmän havaintoarvon välinen erotus. Jos suuruusjärjestykseen asetettua havaintoaineistoa merkitään x(1), x(2),...,x(n), saadaan vaihteluvälin pituudelle kaava d = x(n) - x(1).
 

Vaihteluväli (range)voidaan esittää jo järjestysasteikon muuttujasta. Tällöin ilmoitetaan suurin ja pienin
havaintoarvo R = (x(1) , x(n)).