Harjoi

      Esim.2       

Heitetään rahaa. Tulosmahdollisuudet ovat kruuna ja klaava, joiden todennäköisyydet yhdessä heitossa ovat 0.5 ja 0.5. Toistetaan rahanheitto k kertaa ja mielenkiinnon kohteena on kuinka monta klaavaa saadaan.
Yhdessä heitossa (k=1) nollan klaavan tn=0.5 ja yhden klaavan tn=0.5.

Kahdessa heitossa (k=2) : aina heitoista saadaan 1/2 * 1/2 = 1/4
   0  klaavaa voidaan saada vain yhdellä tavalla: (kr, kr) joten todennäköisyys on 1/4 
   1  klaava voidaan saada kahdella tavalla: (kl, kr), (kr, kl), joten todennäköisyys on 2/4 = 1/2
   2  klaavaa voidaan saada vain yhdellä tavalla: (kl, kl), joten todennäköisyys on 1/4

Kolmessa heitossa (k=3): edelleen tn = 1/2 * 1/2 * 1/2 = 1/8
    0  klaavaa saadaan vain yhdellä tavalla: (kr, kr, kr), joten tn = 1/8
    1  klaava saadaan kolmella tavalla: (kl, kr, kr),(kr, kl, kr),(kr, kr, kl),  joten tn = 3 * 1/8 = 3/8
    2  klaavaa saadaan kolmella tavalla: (kl, kl, kr),(kl, kr, kl),(kr, kl, kl), joten tn = 3 * 1/8 = 3/8
    3  klaavaa saadaan yhdellä tavalla: (kl, kl, kl), joten tn = 1/8

Kun merkitään p:llä onnistumisen todennäköisyyttä yhdessä toistokokeessa (rahanheitossa = 1/2) ja toistojen lukumäärää n:llä, saadaan kombinatoriikan perusteella binomijakauman tiheysfunktioksi



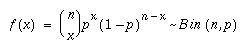
Huomaa, että binomijakaumassa onnistumisen todennäköisyyden ei tarvitse olla 0.5, vaan se saa olla mitä hyvänsä nollan ja yhden väliltä.
Binomijakauma toimii dikotomisten muuttujien mallina, kun tutkitaan esiintyykö jotain asiaa vai ei (esim. sairautta). Toistojen lukumäärää n vastaa havaintojen määrä ja arvioitavana on yhden henkilön sairastumisalttius p, kun otoksesta saatu sairaiden lukumäärä on k.
Binomijakauma on tilastotieteessä tärkein epäjatkuva jakauma. Muita epäjatkuvia teoreettisia jakaumia ovat mm. Multinomijakauma, Poissonjakauma, Hypergeometrinen jakauma ja Geometrinen jakauma.