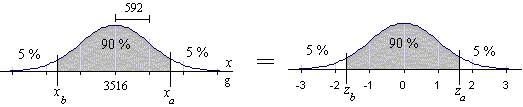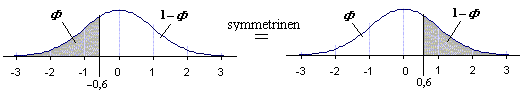Edel:                                                    Hakemisto

    Normaalijakauma

    Esimerkki 2

      Millä todennäköisyydellä syntyvän lapsen paino on yli 4500 g? Normaalijakauma N (3516; 592)
      (Sama kuin: Kuinka monta prosenttia syntyvistä lapsista on painoltaan yli 4500 g?) 
       

      Ratkaisu

      Normitetaan: xa = 4500,  = 3516, s = 592 

      • za = (4500 – 3516) / 592 » 1,66 
      • P (x > 4500) = P (z > 1,66) = 1 – F (1,66) = 1 – 0,9515 = 0,0485 » 4,9 % syntyvistä 
    • MITEN TAULUKKOA LUETAAN? F (1,66) = ? 
    •  

      • z 0 1 2 3 4 5 6 7 8 9
      ... ... ... ... ... ... ... ... ... ... ...
      ... ... ... ... ... ... ... ... ... ... ...
      1,6 ... ... ... ... ... ... 9515 ... ... ...
    • Vasemmassa sarakkeessa on z:n arvosta kokonaisosa ja ensimmäinen desimaali eli 1,6

      • ylimmältä riviltä valitaan toinen desimaali 6. 
    • Alkuosan 1,6 rivin ja toisen desimaalin 6 sarakkeen risteyksestä löytyy kertymäfunktion F arvo 0,9515 
    • Kokonaisosa 0 ja desimaalipilkku on jätetty taulukosta pois selkeyden vuoksi. 
    • Koska normitettu normaalijakauma on symmetrinen, taulukoidaan arvot vain positiivisille z:n arvoille. Negatiivisille z:n arvoille %-arvot päätellään vaihtamalla kuvion oikea ja vasen puoli keskenään symmetrisesti. 
       

    Edel:                                                    Hakemisto

    Normaalijakauma

    Esimerkki 3

  • Millä todennäköisyydellä syntymäpaino on alle 3300 g? 
  • Normitetaan: xa = 3300, 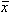 = 3516, s = 592 
    • za = (3300 – 3516) / 592 » –0,36 
    • P (x < 3300) = P (z < –0,36) = F (–0,36) = ??? 
    • Taulukossa ei ole negatiivisia z:n arvoja! 

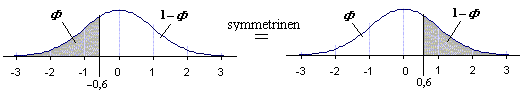
      • symmetrisyyden perusteella 
       
      F (– za) = 1 – F (za)
    • P (x < 3300) = P (z < –0,36) = F (–0,36) = 1 – F (0,36) 

      • = 1 – 0,6406 = 0,3594 » 36 % syntyvistä

Edel:                                                    Hakemisto

  Normaalijakauma

 Esimerkki 4

  • Millä todennäköisyydellä syntymäpaino on yli 2500 g? 
  • Normitetaan: xa = 2500, 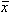 = 3516, s = 592 
  • za = (2500 – 3516) / 592 » –1,72 
  • P (x > 2500) = P (z > –1,72) = 1 – F (–1,72) = ??? 

          • symmetrisyyden perusteella 
       
       
      1 – F (– za) = F (za)
       
        • P (x > 2500) = P (z > –1,72) = 1 – F (–1,72) = F (1,72) (taulukko)

          • = 0,9573 » 95,7 % syntyvistä

    Edel:                                                    Hakemisto

    Normaalijakauma

    Esimerkki 5

  • Millä todennäköisyydellä syntymäpaino on välillä 3000 ... 4000 g ? 
  • Normitetaan: xa = 4000, xb = 3000, 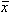 = 3516, s = 592 
    • za = (4000 – 3516) / 592 » 0,82 
    • zb = (3000 – 3516) / 592 » –0,87 
    • P (3000 < x < 4000) = P (–0,87 < z < 0,82) = ??? 

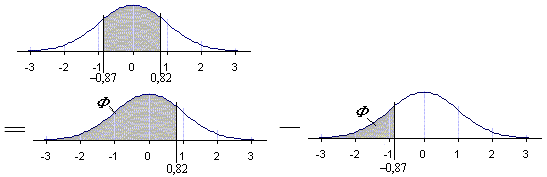
      • Siis P (3000 < x < 4000) = P (–0,87 < z < 0,82) 
      = F (0,82) – F (–0,87) 
      = F (0,82) – [1 – F (0,87)] (taulukko)
      = 0,7939 – [1 – 0,8078] = 0,7939 – 0,1922
      = 0, 6017 » 60 % syntyvistä

    Edel:                                                    Hakemisto

    Normaalijakauma

    Esimerkki 6

  •  Mille painovälille sijoittuu keskimmäinen 90 % syntyvistä lapsista? 
  •  
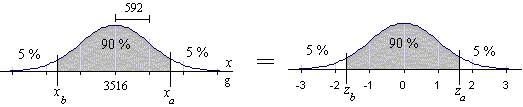  • Ylärajan za alapuolelle jää siis 95 % ja alarajan zb alapuolelle 5 % arvoista 
  • F (za) = 0,95 ja F (zb) = 0,05 
  • P (zb < z < za) = F (za) – F (zb) 
  • Taulukosta etsitään näitä lähinnä olevat arvot 

    •             F (za) = 0,95 » 0,9505
                za = 1,65
                zb onkin za :n vastaluku eli zb = –za = –1,65 
  • Normituskaavasta saadaan 

    •  
    xa = 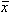 + za · s
    • xa = 3516 + 1,65 · 592 » 4490 (pyöristetään likiarvoksi!!) 
    • xb = 3516 – 1,65 · 592 » 2540 
    Siis keskimmäinen 90 % syntyvistä lapsista sijoittuu välille 2540 ... 4490 grammaa

               Edel:                              Seuraava:                       Hakemisto

    Hosted by uCoz