Heitetään kahta noppaa ja tutkitaan silmälukujen summan todennäköisyysjakaumaa, eli määrätään todennäköisyydet P(X=2), P(X=3), P(X=4),...,P(X=12), missä X on satunnaismuuttuja, joka ilmaisee noppien silmäluvun summan.

Nopat ovat erillisiä ja toisistaan riippumattomia, joten voidaan nimetä toinen noppa 1. nopaksi ja toinen noppa 2. nopaksi. Noppien silmäluvuista ja niiden summasta voidaan esittää taulukko, jossa vaakasuoraan esitetään 1. nopan tulos ja pystysuoraan 2. nopan tulos sekä ruudukon sisällä on silmälukujen summa.

Taulukossa on esitetty kaikki mahdolliset tulokset eli alkeistapausavaruus.

Symmetrisyyden perusteella saadaan määriteltyä nopanheiton silmäluvun todennäköisyysjakauma klassisen todennäköisyyden avulla: lasketaan suotuisten vaihtoehtojen määrä ja jaetaan se kaikkien vaihtoehtojen määrällä. Kaikkaan ruutuja taulukossa on 6*6 = 36, joka on kaikkien vaihtoehtojen määrä.

Todennäköisyysjakauma voidaan esittää myös vaakasuorana taulukkona.

Kertymäfunktio samasta jakaumasta saadaan summaamalla tiheysfuntion pistetodennäköisyyksiä, eli kaavalla

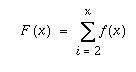
Kertymäfunktio

Todennäköisyysjakauman odotusarvo.

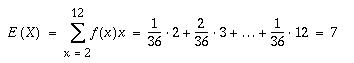
Tämä on tulkittavissa siten, että toistettaessa noppaparin heittoa, saadaan silmälukujen summan keskiarvoksi 7.
Esimerkkejä kuinka tiheys- ja kertymäfunktiota voidaan käyttää apuna todennäköisyyslaskuissa:

a) Millä todennäköisyydellä silmälukujen summa on 6, 7 tai 8 ?

f(6) + f(7) + f(8) = 5/36 + 6/36 + 5/36 = 16/36
tai P(5 < X < 9) = F(8) - F(5) = 26/36 - 10/36 = 16/36

b) Mitä silmälukua pienempiä on 1/3 tuloksista ?

Kun lasketaan kertymäfunktiosta murtoluvut likiarvoiksi saadaan
F(5) = 10/36 = 0.278 ja F(6) = 15/36 = 0.417. Kolmasosa 1/3 = 0.333.
Vastaukseksi saadaan, että 1/3 jakaumasta on alle 7.

Kolme kenttäbiologia etsii rämeiköltä mäkihyppysammakoita toisistaan riippumattomasti. Mäkihyppysammakon havaitsemistodennäköisyys yhdellä kenttäbiologilla on 0.3. Määrää todennäköisyysjakauma sille, kuinka moni kenttäbiologi havaitsee mäkihyppysammakon.

Alkeistapausavaruus on {0,1,2,3} eli 0 vastaa sitä, että yksikään ei havaitse sammakkoa ja 3 vastaa sitä, että kaikki havaitsevat.

Nimetään havainnoitsijat kirjaimilla A, B ja C. Olkoon X satunnaismuuttuja, joka yhdistää havaitsijoiden lukumäärän vastaaviin todennäköisyyksiin.
P(X=0) = P{A ei havaitse ja B ei havaitse ja C ei havaitse}
= P{A ei havaitse}·P{B ei havaitse}·P{C ei havaitse}
= (1 - 0.3)(1-0.3)(1-0.3) = 0.73 = 0.343
P(X=1) = P{A havaitsee ja B ei havaitse ja C ei havaitse} + P{A ei havaitse ja B havaitsee ja C ei havaitse} + P{A ei havaitse ja B ei havaitse ja C havaitsee}
= 0.3·(1-0.3)·(1-0.3) + (1-0.3)·0.3·(1-0.3) + (1-0.3)·(1-0.3)·0.3 = 0.441
P(X=2) = 3 · 0.3 · 0.3 · (1-0.3) = 0.189
P(X=3) = 0.33 = 0.027
Kaikkien tapausten yhteenlaskettu todennäköisyys
P(X=0)+P(X=1)+P(X=2)+P(X=3) = 0.343 + 0.441 + 0.189 + 0.027 = 1.
Todennäköisyysjakauman tiheysfunktiosta ja kertymäfunktiosta voidaan esittää seuraavat kuviot tiheysfunktiosta

ja kertymäfunktiosta

(pystyviivat eivät kuulu kuvioon!).

Jakauman odotusarvoksi saadaan

Tämä on tulkittavissa siten, että koetta toistettaessa havaitsijoiden lukumäärän keskiarvoksi saadaan 0.9.

Tutkitaan koe-eläimen elinaikaa tutkimuksessa (esim. hyönteinen). Maksimielinaika on 1 tunti ja kuolemisen todennäköisyys on sama koko tutkimuksen ajan. Satunnaisesti poimitun koe-eläimen iän todennäköisyysjakauma on määrittelyn mukaan seuraavan kaltainen.
Määrätään a, kun tiedetään, että tiheysfunktion pinta-ala = 1 (eli kaikkien mahdollisuuksien yhteenlaskettu tn = 1). 
 

Kolmion pinta-alan kaavasta saadaan
(1 · a) / 2 = 1 <=> a = 2
Pisteiden (0,2) ja (1,0) kautta kulkevan suoran yhtälö on muotoa f(x) = 2 - 2x, joten tiheysfunktioksi saadaan

Kertymäfunktio määrittelyvälillä 0<x<1 saadaan tiheysfunktion integraalina:

Näet funktion graafisen estyksen klikkaamalla funktiota.
Elinajan odotusarvoksi saadaan