1.2 Tödennäköisyyden idea
Satunnaisilmiön
S tapahtuman
A
todennäköisyydellä tarkoitetaan lukua P(A), joka ilmaisee
odotettavissa olevien A:n sattumiskertojen suhteellisen osuuden S:n tapahtuessa
hyvin monta kertaa.
Klassisen
todennäköiseyyden määrittely edellyttää,
että tulosmahdollisuuksien määrä on äärellinen
ja että tulosmahdollisuudet ovat symmetrisiä. Jos tapausta A
vastaavien symmetristen alkeistapauksien lukumäärä on m,
on todennäköisyys
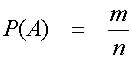
missän on
sattunnaisilmiön S kaikkien alkeistapauksien lukumäärä.
Todennäköisyyslaskennan
peruskäsitteitä
Tapahtumaa
tai ilmiötä, jonka tuloksen määrää sattuma,
kutsutaan satunnaisilmiöksi. Jos se tehdään,
esimerkiksi heitetään noppaa, kutsutaan tekoa satunnaiskokeeksi.
Satunnaisilmiön
mahdollisia tuloksia kutsutaan alkeistapauksiksi ja koko alkeistapausten
joukkoa perusjoukoksi. Perusjoukon osajoukkoa kutsutaan tapahtumaksi.
Tapahtumaan kuuluvia alkeistapauksia kutsutaan suotuisiksi alkeistapahtumiksi.
Jos kaikki
perusjoukon alkeistapaukset ovat yhtä todennäköisyyksiä,
kuten lottoarvonnassa arvotut luvut, kutsutaan alkeistapauksia symmetrisiksi.
Tapahtuma,
jolla ei ole yhtään suotuista alkeistapahtumaa, esimerkiksi nopan
heitossa saada silmäluku 7, kutsutaan mahdottomaksi tapahtumaksi.
Jos kaikki perusjoukon alkeistapaukset ovat suotuisia, tapahtumaa kutsutaan
varmaksi
tapahtumaksi.
TODENNÄKÖISYYS
on tiheysfunktion kuvaajan ja x-akselin väliin jäävän
alueen pinta-ala, eli määrätty integraali.
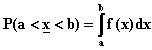 
|