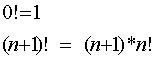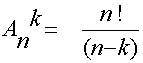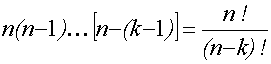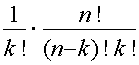1.3 KombinatoriikkaLukun-keroma on n : n ensimmäisen positiivisen kokonaisluvun tulo
N
-positiivisten
kokonaiskukujen joukko. Lisäksi sopimuksen mukaan 0!
= 1. N-kertomavoidaan
induktiivisesti määritellä yhtälöparilla
Permutaatiot JoukonE
= {a1,
a2, . . . an}
permutaatiolla
tarkoitetaan jokaista sen alkioista muodostettava järjestettyä
jonoa, esimerkiksi ( an, an-1, . . . a2,a1
). Lause:
Jos joukossa on n alkiota, niiden permutaatiota on n!. Esimerkki:
3-alkiosella joukolla E
= {a, b, c }
on 3! =
6 permutaatiota: ( a,
b, c)( a, c, b ) ( b,
c, a )( b, a, c ) ( c,
a, b )( c, d, a ) Variaatiot JoukonE
= {a1,
a2, . . . an}
k : ttain muodostettuilla variaatioilla tarkoitetaanE
:
n järjestettyjä osajoukkoja, joissa on k alkiota. Lause:
JoukonE n alkion k : ttain otettujen
variaatioiden määrä on
Todistus seuraa tuloperiaatteesta:1. jäsen voidaan valitan tavalla, 2. jäsen n-1 tavalla jne. Tuloksesi saadaan
Kombinaatiot
JoukonE
= {a1,
a2, . . . an}
k : ttain muodostettuilla kombnaatioilla tarkoitetaanE
:
n josajoukkoja, joissa on k alkiota.
Lause:
JoukonE n alkion k : ttain
otettujen kombinaatioiden lukumäärä on
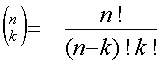 Todistus : k : ttain otettua kombinaatiota vastaa k !variaatiota, joten kysytty kombinatioitten määrä on vain
eli binomikerroin |