| Peruskäsitteet ja laskutoimitukset
Olkoon
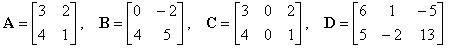
Laske seuraavat lausekkeet tai selitä, miksi niitä
ei ole määritelty.
Olkoon
 , 
,  , 
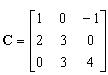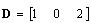
Laske seuraavista lausekkeista ne, jotka on määritelty.
Edellinen
Hakemisto
Vaakarivimuunnokset ja kääntesmatriisin
määrittäminen
| 1.5.1.
Onko jokin matriiseista A , D tai C matriisin X käänteismatriisi,
kun
 
|
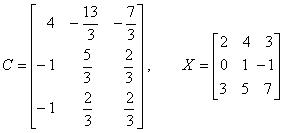
| 1.6.1a) Tutki
onko matriisi
säännöllinen jä myöntiesessä tapauksessa
määritä kääneismatriisia A. |
1.6.8. Jos
matriisin A
alkiot ovat reaalilukuja ja jos
 ,
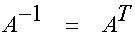niin sanotaan, että A
on ortogonaalinen. Osoita, että tason koordinaatiston kiertoon liittyvä
muunnosmatriisi
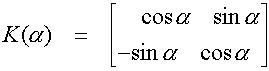
on ortogonaalinen. |
Määritä vaakarivien alkeismuunnoksen avulla
tehtävissä 1.7.4....1.7.7 matriisin A käänteismatriisi,
mikäli sellainen on olemassa
Edellinen
Hakemisto
Laske
käänteismatriisi, mikäli sellainen on olemassa:
Edellinen
Hakemisto
Lineaariset yhtälöryhmät
22. Ovatko seuraavat vektorit
lineaarisesti riippuvia vai riippumattomia?
| a) [1 5 3], [2 4 6], [3 9 11] |
b) [1 1 0], [0 1 1], [1 0 1] |
c) [1 2 3], [4 5 6], [7 8 9] |
| d) [3 0 2 4 5], [7 2 6 1 0], [1 2 2 –7 –10] |
|
|
Determinantit
Laske determinantit:
| 1.8.4a. Olkoot
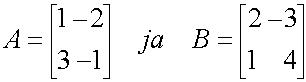
Osoita, että ko. determinantti laskemalla, että
det(AB) =det A det (B). |
| 1.8.4b. Olkoot
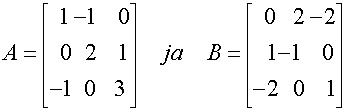
Osoita, että ko. determinantti laskemalla, että det(AB)
=det A det (B).
|
Lineaarisen
yhtälöryhmän matriisiesitys
Edellinen
Hakemisto
| 2.1.1. Ratkaise yhtälöryhmä
matriiseila laskien
|
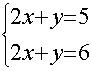
| 2.1.2. Ratkaise yhtälöryhmä
matriiseila laskien
|
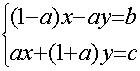
| 2.1.3. Käyttäen
apuna tarkoitukseen soveltuva matemaattista ohjelmistoa ratkaise yhtälöryhmä
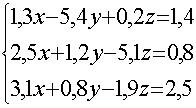
sekä matriiseilla erttä jollain muulla tavalla |
| 2.1.4. Käyttäern apuna
tarkoitukseen soveltuvaa matemaatista ohjelmistoa yritä ratkaista
yhtälöruhmä
|
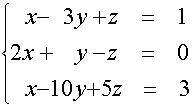
Edellinen
Hakemisto
Pienimmäm summan menetelmä
Määritä yhtälöryhmän 2.3.1
. . . 2.3.4 pienimmän neliösumman ratkaisut
Edellinen
Hakemisto
2.3. 5. Tiedetään,
että y = kx + p. Määritä pienimmän
neliösumman menetejmällä likiarvot k:n ja
p:n arvolle, kun on käytettävissä mittaustulokset
| x |
0 |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
| y |
1.0 |
1,8 |
2,5 |
3,3 |
3,9 |
4,5 |
5,1 |
2.3. 6.
Tiedetään, että
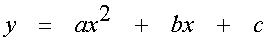
ja on käytettävissä mittaustulokset
| x |
-0,8 |
0,5 |
1,4 |
1,7 |
2,5 |
2,5 |
2,7 |
| y |
0,5 |
1,4 |
1,8 |
2,0 |
2,0 |
1,6 |
1,5 |
Määritä normaaliyhtälön avulla likiarvot
a:n , b:n , ja c:n arvoille. Esitä myös
samassa koordinaatistossa sekä mittauspisteet että määrittämäsi
pienimmän neliösumman paraabeli |
Edellinen
Hakemisto
2.3. 7. Tiedetään,
että y = f(x) ja käytettävissä on mittaustulokset
| x |
-1,0 |
0 |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
9,0 |
| y |
1,1 |
1,2 |
2,0 |
3,2 |
4,0 |
3,8 |
3,1 |
1,9 |
0,5 |
-3,0 |
-7,0 |
Muodosta x:n ja y:n riippuvuutta kuvaava matemaattinen
malli valitsemalla sopivat kantafunktiot f1, f2, . . . , fp ja etsimällä
kertoimet
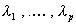siten, että malli
ja havainnot sopivat mahdollisimman hyvin yhteen. Pirra samaan koordinaatistoon
havaitopisteet ja |
Ominaisarvot ja ominaisvektorit
Laske seuraavien matriisien ominaisarvot ja ominaisvektorit.
Edellinen
Hakemisto |
